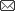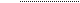|
|
MIT Press 1996 Book Chapter on Phased Array Optics The following book chapter from Nanotechnology: Molecular Speculations on Global Abundance, Editor BC Crandall (MIT Press,1996) first popularized the long-term potential of phased array optical technology. It is reproduced here with permission of MIT Press. Phased Array OpticsThe Future in Sight by Brian Wowk (Oct. 3, 1991) The year is 2020. You are standing on a platform at the edge of a thousand foot cliff overlooking the Tharsis volcano range on Mars. Your body casts a long shadow in the light of the setting sun as you scan the horizon for interesting features with your binoculars. Walking toward the edge of the precipice, you survey the texture of the rusty red boulders around you. Butterflies rise in your stomach as you peer over the cliff edge. Sixteen hundred miles overhead, Phobos, one of the Martian moons shines conspicuously. There is a new transport base under construction there. You move toward your telescope to get a better view, when suddenly a doorway materializes out of empty space! A leg steps through it. It's your wife with dinner. Of course, you were never really on Mars. The "platform" you were standing on was merely the floor of a small, comfortably furnished room called a teleporter. The walls and ceiling of this room are covered with one of the technological wonders of the 21st century: phased array optics. TheoryPhased array optics is a technology that will produce three dimensional views of objects and scenery using only two dimensional displays. Display systems based on this technology-- optical phased arrays --will behave quite literally as windows onto whatever scenery we can imagine. Phased arrays are based on the theory of diffraction from physical optics. This theory says that patterns of light waves travelling beyond an aperture (such as a window) are entirely determined by the amplitude and phase distribution of light at the surface of the aperture. This means that if we produce light with the right phase and brightness distribution across a two dimensional surface, we can reproduce the same light waves that would emanate from a three dimensional scene behind the surface. In other words, we can make that surface appear as a window onto the scene. Diffraction theory is mathematically continuous; it is assumed that surfaces can be reduced to an infinite number of small elements radiating with different amplitude and phase. This introduces complications from the standpoint of developing a practical technology. Fortunately we can achieve the same results with a discrete array of sources, provided they are coherent and less than 1/2 wavelength apart. The wavelength of visible light ranges from 0.4 microns (violet) to 0.7 microns (red). A two dimensional array of programmable sources 0.2 microns apart will therefore be sufficient to reconstruct any light wave pattern we desire. Figure 1 illustrates the reconstruction principle in two dimensions for a few simple cases. In Fig. 1(a) all the sources radiate with the same amplitude and phase. Their waves interfere to create a plane wave propagating normal to the surface. This is the type of wave that would be produced by a distant point source. In Fig. 1(b) there is a linear variation of phase among the sources down the line. The result is a plane wave propagating at an angle to the surface. By adjusting the amount of phase variation, we can "steer" this beam in any direction we please. In Fig. 1(c) a more complicated phase relationship is used to produce a spherical wave, creating the image of a point source near the surface.
By choosing the correct phase and amplitude distribution across the array we can, in fact, create images of any number of points at any number of locations behind the array. Since any three dimensional scene can be represented as a collection of discrete points in space, it follows that our array can reproduce any three dimensional scene. The procedure for calculating the phase and amplitude distribution required to produce a scene is straightforward. All visible objects in the scene are represented in a computer in terms of discrete surface points. The spacing of the points is determined by the resolution of the array. Each point is assumed to produce a spherical wave. The complex amplitudes of these waves are summed at each source position on the array. The resultant complex amplitude at each source point determines the phase and intensity that source must radiate to reproduce the scene. DesignThe sources in a phased array must radiate coherently. That is, they must be able to interfere with each other. The easiest way to achieve this is to illuminate the back of the array with light from a single laser. A diverging laser beam could be aimed at the array from behind, or the beam could be transported through a thin planar waveguide on the rear surface of the array. Since lasers can be made with coherence lengths of kilometers, it doesn't really matter how the laser light gets to the sources. It will always be coherent across the array, and each source can have its own phase and amplitude calibration factors. In this scheme, each "source" in the array is a passive transmission element with adjustable optical path length (phase) and transmission (amplitude). Fig. 2 shows a cross section through a few elements. The elements are 0.2 microns (2000 angstroms) apart. (A bacterium could cover five of them.) Each element consists of a phase shifter and an amplitude modulator.
The amplitude modulator is simple. A cross polarizer like those in LCD displays should suffice. The phase shifter is made of an electrooptic birefringent material. This means that the shifter changes its refractive index along one polarization direction in response to an electric field. A polarizing filter down the back of the array ensures light of the proper linear polarization enters the shifter. A quarter wave plate on the front of the array to restore elliptical polarization is optional. A large variety of crystals are known to exhibit the required electrooptic effect (Kaminow 1974). Some of these are semiconductors that are the stock in trade of existing microfabrication technology. Unfortunately the electrooptic effect in solid crystals is rather weak. Even very large electric fields produce very small changes in refractive index. Since each phase shifter must be able to retard light passing through it by one full wavelength, a small change in refractive index means a long phase shifter. For solid crystals this length will be on the order of a millimeter, which is probably too long to be practical. Nematic liquid crystals exhibit an electrooptic effect thousands of times stronger than that found in solids (Kahn 1972). If these crystals can be made with a high refractive index and fast response, then phase shifters one micron long like those in Fig. 2 should be possible. An interesting alternative has been suggested by Jeffrey Soreff of IBM (Soreff 1991). Rather than relying on electrooptic effects, a crystal with a large fixed birefringence, such as calcite, could be used. The crystal is sandwiched between parallel linear polarizers, and rotated relative to the direction of polarization. The phase-shifting rotation could be accomplished by mechanical rotation of the crystal, or by rotating the polarizer directions. This scheme would also permit micron length phase shifters. In all these designs each phase shifter is behaving as a waveguide near cutoff. Red light, with a wavelength in free space of 0.6 microns, will be the most difficult to deal with. To get through a waveguide less than 0.2 microns wide, its wavelength will have to be reduced to less than 0.4 microns. This will require a refractive index of at least 1.5 in the phase shifting medium. Data ManagementWhile the synthesis of array images may be mathematically simple, it will be computationally severe (by 1991 standards). A source separation of 0.2 microns gives 25 million sources per square millimeter, 2.5 billion per square centimeter, and 25 trillion array sources per square meter. Each one of these sources will have to radiate with its own calculated phase and amplitude. This is a staggering amount of information. To understand the origin of this information, recall that the array behaves as a window onto the scene it is reproducing. Suppose a square meter array is reproducing a wilderness scene. Looking through the array, one sees a meadow, a small lake and a mountain beyond. One mile away, on the far shore of the lake, a man is fishing. If you aimed a telescope in his direction you would see him clearly. And if you had a really big telescope (one with a two foot wide lens) you would be able to see a housefly on his hat. It is now obvious why the array contains so much information. A meter wide array (or window for that matter) has a diffraction limited resolution of about one millionth of a radian, or 0.2 seconds of arc. The array image therefore contains every scene element subtending a solid angle greater than a trillionth of a steradian: the fly on the man's hat, leaves on trees five miles away, most every blade of grass in the meadow, and so on. The number of scene elements recorded by an array is roughly equal to the number of sources in the array. To compute the phase and amplitude for each source, we must add the contributions of spherical waves from each scene element to each source point. For a square meter array, this is 1000 trillion trillion floating point operations. A single computer would have trouble finishing this calculation within the lifetime of the universe. Fortunately several considerations come to our rescue. First, this type of calculation is amenable to Fast Fourier methods, which tend to reduce N squared operations to NlogN operations (a trillion fold decrease in our case). Second, this problem is well suited to massive parallelism. With enough processors, there is no reason why array image synthesis couldn't proceed at movie frame rates. Finally, not all array images will require resolution beyond that of the unaided eye. This concession alone reduces the computation and bandwidth requirements by several orders of magnitude. Real time arrays still pose formidable data storage and transmission problems. A square meter array operated at human eye resolution will require about a gigabyte per frame, or 50 gigabytes per second. Interestingly light itself is ideally suited to transmission at this rate. Modulated light could be used for both long distance transmission and local control of array sources. Instead of trillions of tiny wires, light traveling through the same waveguide as the primary laser could carry image information to decoders at periodic intervals in the array. The data storage requirements of arrays cannot yet be met economically. (A phased array movie would consume several hundred terabytes!) Nevertheless, storage technologies able to handle arrays are on the horizon. Certainly molecular technology, with its promise of 1 gigabyte per cubic micron (Drexler 1986, 247), will be more than sufficient. Phased Arrays vs. HolographyPhased arrays and holography are both methods of wavefront reconstruction, and both can produce three dimensional images. However they differ in some important ways. Holography avoids the computational requirement of arrays with a simple and elegant solution. The scene to be reproduced is illuminated with a laser. A photographic film is placed near the scene to capture reflected light (the "object" beam). At the same time, a reference beam from the same laser is shone on the film. Because they come from the same laser, the object and reference beams are coherent and produce a microscopic interference pattern which is recorded on the film. This interference pattern is analogous to the phase and amplitude modulation of sources in a phased array. When a laser beam is shone on the developed film, the transparent areas of the interference pattern select out those parts of the beam that have the correct phase to reconstruct the recorded scene. Holography is simple and works without a computer, however it has inherent drawbacks. Holographic recording produces phase modulation that is too coarse for unambiguous wave reconstruction. When you shine a laser on a hologram you will always get three beams out: the reconstructed object beam, the (unwanted) conjugate beam, and the laser beam itself. This happens because of the wide spacing of interference fringes produced by holographic recording. (The three beams are actually three orders of diffraction.) Phased arrays modulate phase and amplitude at half wavelength intervals. This is close enough to generate only one interference maximum, which contains the reconstructed beam and nothing else. Simulated IncoherencePhased arrays reproduce scenery using coherent light. This raises certain problems that have been glossed over so far. It was assumed earlier that different parts of a scene could be reproduced independently. This is not quite true for coherent light. Light waves from different points in a coherent scene would interfere with each other, generating unnatural effects such as laser speckle. A simple solution exists. Numerous separate versions of a scene could be synthesized, each assigning a different random phase factor to points in the scene. When presented in rapid succession (say 20 versions per second) all interference effects would blur out, creating an effectively incoherent scene. In terms of eliminating laser speckle, this process is equivalent to rapidly altering the microscopic structure of a scene surface. ColorProducing colored scenes is easy. Three versions of each scene would be synthesized in red, green, and blue light (the three primary colors of human vision). The array would cycle through them rapidly, alternating between red, green, and blue lasers. Because scenes would tend to split apart into separate colors if you moved your eyes fast, you would want a fast cycle time (ideally less than a millisecond). Although they would appear perfectly authentic to human eyes, scenes produced in this way would be easily detectable by a prism. They might not fool animals either. The ultimate solution is to cycle very quickly through the entire visual spectrum at random increments. Such an array would be difficult to detect. Transparent ArraysIf a transparent planar waveguide is used to carry laser light across the back of a phased array, then the array will be semitransparent with perhaps 30% transmittance (like tinted glass). This raises all sorts of interesting possibilities. For one, the array could superpose images on real scenery behind it. (A glide path for a landing aircraft is a nice example.) More profound, though, is what the array could do to the scenery itself. In the theory of diffraction, most every element of an optical system can be modelled as a two dimensional surface with a complex transmission function. (A lens, for example, is equivalent to a flat surface with particular phase changing properties.) Phased arrays will turn this mathematical abstraction into technological reality. A single transparent array could behave as a programmable phase plate, fresnel zone plate, hologram, prism, diffraction grating, or variable focal length low f number diffraction limited lens. All this from an array microns thick, and able to change roles in a microsecond. You could hold such a thing in your hand, and swear it was from another world. The Recording ProblemFor many applications the scenery produced by an array will originate entirely in a computer. When it doesn't, a way must exist to record real scenery that allows reproduction by an array. In the general case of an incoherent (naturally illuminated) scene, the only way to do this is brute force: record conventional flat images from every angle you can get. For low resolution reproduction, a "fly's eye" lattice of one centimeter wide lenses would be used to record multiple views of a scene. A computer would then infer the three dimensional structure of the scene from these views, and proceed with image synthesis by methods already discussed. This system would have adequate resolution for viewing with the unaided eye. Higher resolution would require bigger lenses. Transparent arrays are well suited to this application. A transparent array could behave as a fly's eye lens to record nearby objects, and later become a single huge lens to record details miles away. This type of system could quickly gather all the information needed to reproduce scenes with telescopic resolution. High Power ArraysThe array designs presented so far operate by modulating laser light passing through them. The "sources" don't actually produce light themselves. For some applications, particularly outdoor use, a higher power design is desirable. The visual intensity of the sun (about 500 watts per square meter) is the regime we seek. Consider putting a tiny laser at the base of each phase shifter. (Quantum well semiconductor lasers would be ideal.) These lasers provide a coherent boost to light passing through the array, essentially transforming the whole array into a resonant cavity. In other words, the array becomes one big laser with adjustable emission phase across its surface. Color could be dealt with by making the lasers tunable, or by laying them out in a red-green-blue hexagonal lattice. Now consider a building covered on all sides by a high power phased array. By day it could produce an image of a landscape contiguous with its surroundings, thereby rendering itself effectively invisible. By night it could do more of the same, or, for variety, create the image of a floodlit building. Perhaps it would supplement this scene with the image of a powerful, sweeping searchlight to detect and/or intimidate intruders. For those occasions when the searchlight was not intimidating enough, it could match the phase of a few array sources relative to an intruder. Matching the phase of sources in a phased array has interesting consequences. Suppose an observer looking at the array sees one square meter worth of sources radiating at exactly the same phase relative to him. The sources will interfere constructively, depositing their entire output energy to a very small point at his location. In other words, the observer will be at the focus of a one kilowatt laser (not a very healthy place to be). Of course the same principle can be employed over the entire surface area of the building, encompassing hundreds of kilowatts of laser power. Our camouflage, decorative lighting system is now a long-range missile defense system, or directional transmitter of interstellar range. (With a beam divergence less than a millionth of a degree, a stable 100 meter wide array would appear 1% as bright as the sun at any distance.) While this example is a bit extreme, it illustrates that very small coherent sources can give very big laser power. It follows that generating images of lasers and laser light will be an important application of phased arrays (particularly in view of the high efficiency of semiconductor lasers). Advanced ApplicationsDisplaying still scenery matching your surroundings is one form of invisibility. We could call this passive invisibility. With a view toward very fast and compact computers, an even more audacious possibility exists: active invisibility. Active invisibility means an array would acquire and synthesize contiguous scenery in real time. This could be accomplished with a system a few millimeters thick. The interior layer of our hypothetical "invisibility suit" consists of photosensors comparable to a human retina. The exterior is a phased array with phase shifters of extra close spacing and high refractive index. Half of the shifters are dedicated to image production, while the other half transmit light through to the photosensitive layer. The transmitting shifters are adjusted to form a multitude of focussed "fly's eye" images on the photosensitive layer. The system is thus able to both produce and view scenery from all angles at the same time. A powerful computer network would manage the scenery synthesis and other details, such as how suit movement affected phase relationships. Other designs are possible. Such speculations lie at the limits of foreseeable technology. It is nonetheless amazing that something as fantastic as invisibility could be achieved using known science. Front Projection ImagesPhased arrays can produce images of objects anywhere in space behind them. But that is not all they can do. With certain restrictions, they can also make objects appear IN FRONT of them. Figure 3 illustrates the principle for a point source. By producing converging spherical waves, the array has created the image of a point source in front it. Once again, creating a whole object is just a matter of assembling the points which comprise it. By controlling which areas of the array reproduce various points, hidden lines and surfaces are removed, and even front-projected objects will appear solid and opaque.
Imagine you are back in your teleporter room enjoying the Martian panorama. This time the floor is also covered with phased array optics. Martian boulders now appear at your feet, amongst the furniture, and in one case right in front of your nose! Now that's realism. Virtual teleporters covered on all sides by phased arrays bear a striking similarity to the "holodeck" concept of Star Trek. Anything could happen in such a room. Anything. The FutureOptical phased arrays pose substantial challenges of information processing and nanofabrication. Nevertheless it seems certain that these challenges will be met within the next twenty to thirty years. Some precursor technologies, such as LCD holography, are at the edge of even current capability. Over the long term, the future of arrays is as limitless as imagination itself. The few applications mentioned here are just a glimpse of their potential. As Arthur C. Clarke recently said about virtual reality (Rheingold 1991), this technology "won't merely replace TV. It will eat it alive." REFERENCES:Kaminow, I.P. 1974, An Introduction to Electrooptic Devices, Academic Press. Kahn, F.J. 1972, Electronically Tunable Birefringence, U.S. Patent 3,694,053 assigned to Bell Telephone. Soreff, J. 1991, private commication. Drexler, K.E. 1986, Engines of Creation, Anchor Press Doubleday. Rheingold, H. 1991, Virtual Reality, Summit Books. About the Author:In 1991 Brian Wowk was a graduate student in the medical physics program at the University of Manitoba in Winnipeg, Canada. His interests included medical imaging and the medical application of nanoscale technologies, and still do. | ||||||||||||||||||||||
|
 |